Menghitung volume cairan pada tangki silinder horisontal
kita buat penampang melintang, seperti pada gambar di bawah ini, dengan ketinggian
cairan pada tanki adalah variabel yang tergantung terhadap volume cairan pada tanki
(dimana volume terikat terhadap variabel jari – jari tanki).
Untuk mempermudah kalkulasi, variabel volume cairan tanki direpresentasikan dalam
bentuk rasionya dengan volume cairan maksimal pada tanki (x) atau x = volume cairan
pada tanki / volume maksimal cairan pada tanki.
Untuk perhitungan selanjutnya, perlu untuk dibentuk persamaan yang sesuai dengan
kondisi, x < 0.5 dan x > 0.5. Berikut ringkasannya.
Untuk x < 0.5, persamaan dapat berangkat dari volume cairan pada tanki adalah volume juring ABCO dikurangi volume segitiga ACO. persamaan dapat diperhatikan
pada gambar berikut .
(persamaan dibagi dengan panjang tanki).
Dengan bentuk fungsi sudutnya adalah sebagai berikut .dan berikut bentuk persamaan untuk h (ketinggian cairan dalam tanki)
Sedangkan untuk kondisi x > 0.5, persamaan dapat dibentuk dengan pertama –
tama memutar 180 derajat gambar tanki di atas. Jadi, volume cairan tanki adalah
volume maksimal cairan tanki di kurangi volume busur ABCD. Dengan volume
busur ABCD adalah volume Juring ABCO dikurangi volume segitiga ACO.
Berikut bentuk fungsi sudut dan persamaan h untuk kondisi x > 0.5.
Untuk kalkulasi nilai sudut, metode iterasi Newton – Raphson dapat digunakan
dengan menggunakan fungsi sudut yang sudah diturunkan. Berikut bentuk
sederhana dari metode Newton – Raphson.
dengan bentuk turunan fungsi sudut seperti pada gambar berikut.
Sedangkan untuk kondisi x = 0, x = 0.5, dan x = 1, nilai sudutnya dapat langsung
ditentukan yang adalah, masing – masing, 0 derajat, 90 derajat, dan 180 derajat
(atau 90 derajat jika gambar tanki di atas dibalik, yang sesuai dengan asumsi
untuk penurunan persamaan fungsi sudut pada kondisi x > 0.5).
Oke cukup dulu uraian tahapan logika fungsi sudut, untuk mencoba
mari kita ambil contoh perhitungan :
Diketahui :panjang tangki = 200 cm, r (jari2)= 50 cm, tinggi cairan = 75 cm,
LUAS LINGKARAN = 3,14 x 50 x 50 = 7850
AKAR LEBAR PERMUKAAN CAIRAN
= (r x r) - ((t-r) x (t-r))
= (2500) - ((75-50) x (75-50))
= (2500) - (25 x 25)
= 2500 - 625
= 1875
AKAR = 43,3012
LUAS 2 SEGITIGA = AKAR x (t-r)
= 43,3012 x 25
= 1082,53
a sin = (AKAR : r)
= 43,3012 : 50
= 0,866024
a sin = 59,999839
LUAS POTONGAN KUE = ((a sin x 2) :360) x luas lingkaran
= ((119,999678) : 360) x 7850
= 0,333332438 x 7850
= 2616,6596
LUAS BUSUR = LUAS POT KUE - LUAS 2 SEGITIGA
= 2616,6596 - 1082,53
= 1534,1296
LUAS CAIRAN = LUAS LINGKARAN -LUAS BUSUR
= 7850 - 1534,1296
= 6315,8704
VOLUME CAIRAN = LUAS CAIRAN x PANJANG TANGKI
= 6315,8704 x 200
= 1263174,08 cm3 = 1263,1 liter
Ada sedikit perbedaan hasil antara perhitungan manual di atas dibandingkan
dengan menggunakan tools aplikasi di bawah ini, yaitu sebesar 0.6 liter.
Perbedaan itu dikarenakan pembulatan nilai antara PC dan kalkulator.
Agak rumit memang tapi ada rumus yang lebih simple , anda bisa menggunakan
seperti di bawah ini :
mari kita ambil contoh perhitungan :
Diketahui :panjang tangki = 200 cm, r (jari2)= 50 cm, tinggi cairan = 75 cm,
LUAS LINGKARAN = 3,14 x 50 x 50 = 7850
AKAR LEBAR PERMUKAAN CAIRAN
= (r x r) - ((t-r) x (t-r))
= (2500) - ((75-50) x (75-50))
= (2500) - (25 x 25)
= 2500 - 625
= 1875
AKAR = 43,3012
LUAS 2 SEGITIGA = AKAR x (t-r)
= 43,3012 x 25
= 1082,53
a sin = (AKAR : r)
= 43,3012 : 50
= 0,866024
a sin = 59,999839
LUAS POTONGAN KUE = ((a sin x 2) :360) x luas lingkaran
= ((119,999678) : 360) x 7850
= 0,333332438 x 7850
= 2616,6596
LUAS BUSUR = LUAS POT KUE - LUAS 2 SEGITIGA
= 2616,6596 - 1082,53
= 1534,1296
LUAS CAIRAN = LUAS LINGKARAN -LUAS BUSUR
= 7850 - 1534,1296
= 6315,8704
VOLUME CAIRAN = LUAS CAIRAN x PANJANG TANGKI
= 6315,8704 x 200
= 1263174,08 cm3 = 1263,1 liter
Ada sedikit perbedaan hasil antara perhitungan manual di atas dibandingkan
dengan menggunakan tools aplikasi di bawah ini, yaitu sebesar 0.6 liter.
Perbedaan itu dikarenakan pembulatan nilai antara PC dan kalkulator.
Agak rumit memang tapi ada rumus yang lebih simple , anda bisa menggunakan
seperti di bawah ini :
Tetapi jika anda tidak ingin repot dan pingin yang lebih mudah lagi, maka anda bisa
Pesan untuk menggunakannya, janganlah memberi nilai masukan Tinggi cairan
melebihi nilai 2 x Jari jari.
Berikut ini alamat link downloadnya (88 kb) melalui googledrive :
http://www.4shared.com/rar/XuzZ7_2i/Tangki_horisontal.html
Sekian postingan hari ini, sampai ketemu pada postingan berikutnya,
Menghitung volume tangki ellips, yang mempunyai ukuran tinggi dan lebar berbeda.




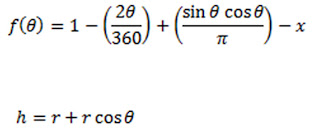



No comments:
Post a Comment